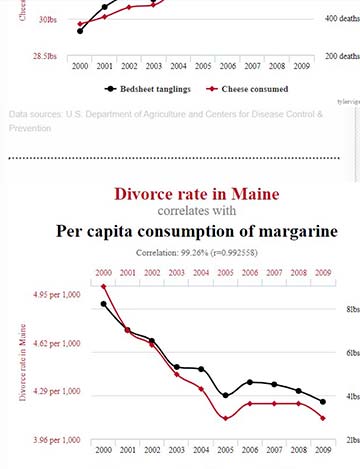
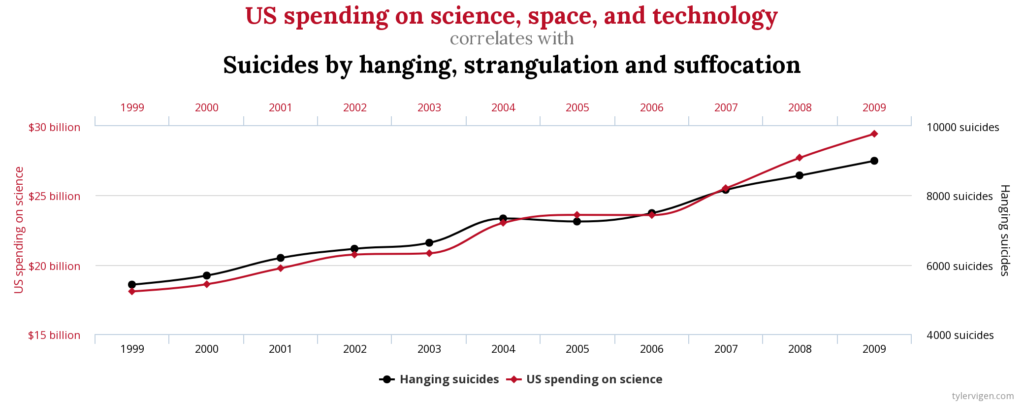
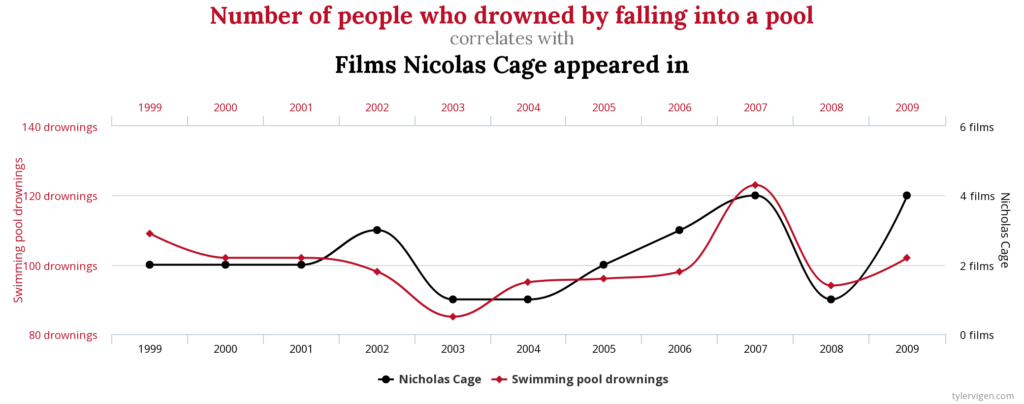
In statistics, a spurious relationship or spurious correlation is a mathematical relationship in which two or more events or variables are associated but notcausally related, due to either coincidence or the presence of a certain third, unseen factor (referred to as a “common response variable”, “confounding factor”, or “lurking variable”). wikipedia
Very large databases are a major opportunity for science and data analytics is a remarkable new field of investigation in computer science. The effectiveness of these tools is used to support a “philosophy” against the scientific method as developed throughout history. According to this view, computer-discovered correlations should replace understanding and guide prediction and action. Consequently, there will be no need to give scientific meaning to phenomena, by proposing, say, causal relations, since regularities in very large databases are enough: “with enough data, the numbers speak for themselves”. The “end of science” is proclaimed. Using classical results from ergodic theory, Ramsey theory and algorithmic information theory, we show that this “philosophy” is wrong. For example, we prove that very large databases have to contain arbitrary correlations. These correlations appear only due to the size, not the nature, of data. They can be found in “randomly” generated, large enough databases, which—as we will prove—implies that most correlations are spurious. Too much information tends to behave like very little information. The scientific method can be enriched by computer mining in immense databases, but not replaced by it.
Spurious Correlations is a project by Tyler Vigen that put together to look at correlations and to think about data. The charts on his site aren’t meant to imply causation nor are they meant to create a distrust for research or even correlative data.
Visit Spurious Correlations
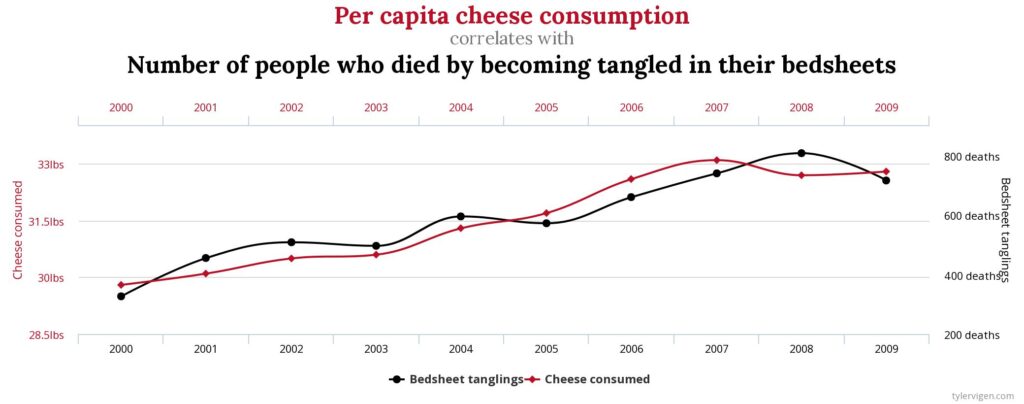
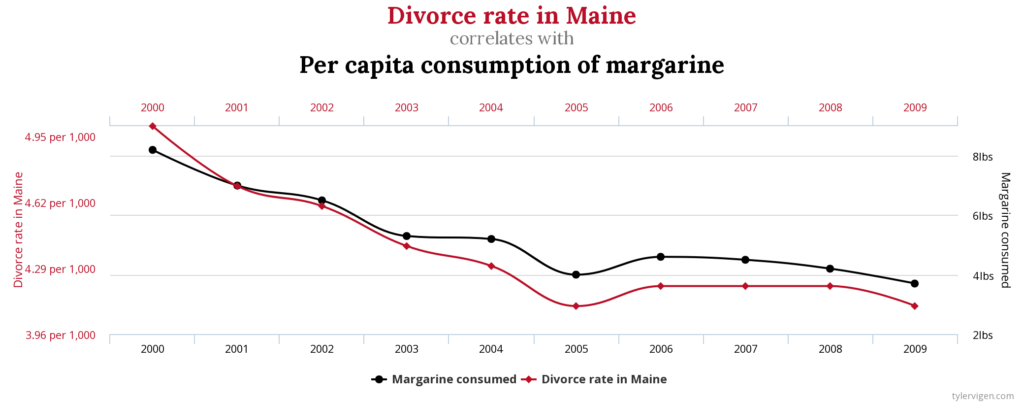
Visit Spurious Correlations
Further readings
Cristian Calude, Giuseppe Longo. The Deluge of Spurious Correlations in Big Data. Lois des dieux, des hommes et de la nature, Oct 2015, Nantes, France. pp.1 – 18, ff10.1007/s10699-016-9489-4ff. ffhal01380626f
DOWNLOAD